Introduction

In previous presentations, we [AR, AvM] talked about stochastic differential equations (middle box in Fig. 1). Examples:

Brownian motion

\(\dot{X}(t) = ξ(t)\)

\(X(t) = \mathcal{N}(0, t)\)

Brownian motion

\(\dot{X}(t) = ξ(t)\)

\(X(t) = \mathcal{N}(0, t)\)

Drift-diffusion processes

\(\dot{X}(t) = f(t,X) + ξ(t)\)

\(dX(t) = f(t,X)dt + g(t,X)dW\)

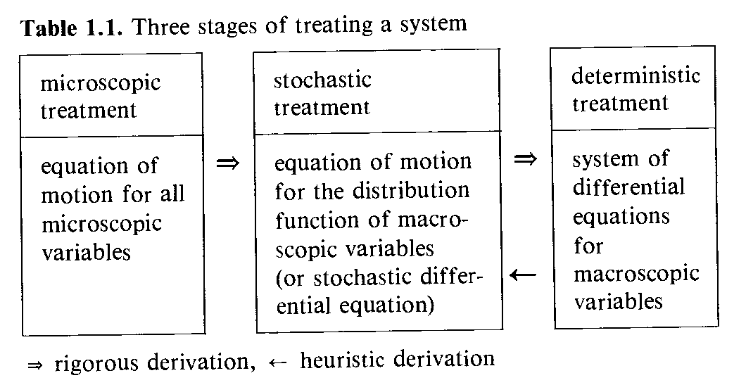
Fig. 1 (Risken, Table 1.1)

We also talked about the fact that the “white noise” \(ξ\) in a Langevin equation is ill-defined.

Note

All of these conventions are defined in terms of finite intervals.

Itô convention

\[ΔX(t_i) = f(t_i,X(t_i))Δt + g(t_i,X(t_i))ΔW(t_i)\bigr)\hphantom{+ g(t_{i+1},X(t_{i+1}))}\]

Stratonovich convention

\[ΔX(t_i) = f(t_i,X(t_i))Δt + \frac{g(t_i,X(t_i)) + g(t_{i+1},X(t_{i+1}))}{2}ΔW(t_i)\]

Anticipatory (or Hänggi-Klimontovich) convention

\[ΔX(t_i) = f(t_i,X(t_i))Δt + g(t_{i+1},X(t_{i+1}))ΔW(t_i)\hphantom{+ g(t_{i},X)}\]

This ambiguity of convention arises because the infinitesimal limit of white noise is mathematically well-defined (within a given convention), but non physical.

A full solution to a Langevin equation typically takes the form of a probability density function (PDF), which, if the system is Markovian, can be written as \(p(t, X)\). Now, this PDF is physical, so a differential equation for \(p(t, X)\) should not suffer from ambiguity. The Fokker-Planck equation is such a differential equation:

(1)\[ \frac{\partial p(t, x)}{\partial t} = - \sum_i \frac{\partial}{\partial x_i} \left[D_i^{(1)}(x) \, p(t,x)\right] + \sum_{i,j} \frac{\partial^2}{\partial x_i \partial x_j} \left[D_{ij}^{(2)}(x) \, p(t, x) \right] \]

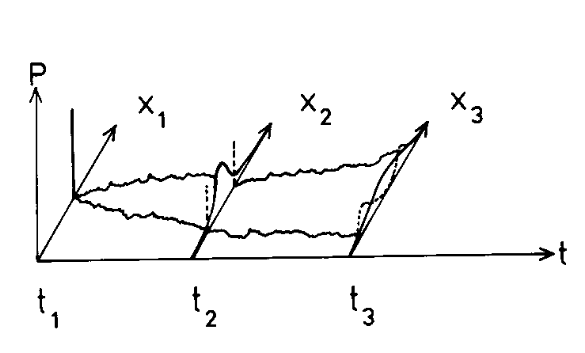
Fig. 2 The kind of problem we want to solve: given an initial probability distribution, how does it evolve over time ? Often, but not always, the initial condition is a Dirac δ. (Risken, Fig. 2.2)

A stochastic process is a generalization of a random variable. Intuitively, we assign to each \(t \in \mathbb{R}\) a random variable (as suggested by Fig. 2). More precisely, to any countable set of times, the process associates a joint distribution. So if \(x \in \mathbb{R^N}\),

• \(p(t_1, x_1)\) is the PDF of a random variable on \(\mathbb{R}^N\);

• \(p(t_2, x_2, t_1, x_1)\) is the PDF of a random variable on \(\mathbb{R}^{2N}\);

• \(p(t_3, x_3, t_2, x_2, t_1, x_1)\) is the PDF of a random variable on \(\mathbb{R}^{3N}\);

• etc.

One obtains a lower dimensional distribution by marginalising over certain time points:

\[p(t_3, x_3, t_1, x_1) = \int p(t_3, x_3, t_2, x_2, t_1, x_1) dx_2\]

Markov process: \(p(t_3, x_3 \mid t_2, x_2, t_1, x_1) = p(t_3, x_3 \mid t_2, x_2)\)

For a Markov process, this becomes the Chapman-Kolmogorov equation:

\[p(t_3, x_3 \mid t_1, x_1) = \int p(t_3, x_3 \mid t_2, x_2) p(t_2, x_2 \mid t_1, x_1)\]